How Computers Work: The Logic behind!

When I say "world-changing", what is it that comes to your mind? Discoveries? Pandemics? People?

Of all these, there is one invention that changed the modern world the most: Computers!

What makes the world today different from that of the 18th century or even before that? The use of computers and the services possible through computers, like the Internet! 

Computers are made to automate every aspect of human life and maybe eventually represent humans itself. 

They are controlling everything in the modern world. From making a phone call, to heavy calculations, discoveries, and implantations within humans! 

The breakdown of a Computer (No, not emotional one, it is not stressed):

Let's start with what a computer is. According to Oxford Languages, "A computer is an electronic device for storing and processing data, typically in binary form, according to instructions given to it in a variable program."

 

Let's break the definition down:

• A computer is an electronic device, which runs on electric energy supplied externally. Why? Because a computer does physical work and doing physical work requires energy. Simple conservation laws acting there.

• Next thing is that "a computer stores and processes data". A very important aspect of human intelligence is memory. We can remember data and use it to analyse patterns and go about our daily work. Modern computer circuits are just like a human brain. They have memory! Now, by memory I do not mean storage. Devices like optical drives or magnetic hard disks cannot give a computer its memory. Memory is the intrinsic property of a circuit to remember data and actively process it. Memory and processing go hand-in-hand. Storage is when the processed data is no longer needed and can be saved in a storage device. For a comparison, memory is when you've been asked to bring your classwork notebook to school and forget easily. Storage is when you write it down in your school diary and can stop worrying about remembering it. Storage devices are much simpler to make than achieving memory. Similar to how easy it is to make a diary than neural circuits in your brain for memory. The neural circuit counterpart for computers are 'Logic Gates' (explored later in the article!).

• Computer circuits don't work unless a program asks it to do so.

• A program is a set of instructions, written in a special language, to communicate with a computer. For writing a program, an algorithm (or logic) has to be decided first on the basis of which a program would work. These instructions are what tells the computer what to do. A computer doesn't understand human languages. Languages have been developed by humans in which a program can be passed on to a computer. These are known as  programming languages and can be used to code any set of instructions by humans, like a program (aka app here) to text someone. 

The language of Gods, uh, I mean...Computers: 

A little detail I skipped is that computer circuits are electronic machines so only understand electric signals. There can be two states of an electrical signal: on(high voltage state) or off(low voltage state). To interpret the high/low voltage states, a language was needed. Base 2 number system or binary digits turned out to be the best choice since it only has 2 digits: 1 and 0. On state was assumed to be a 1 and off state was assumed to be a 0. Now, just two digits cannot solve problems using normal high-school algebra since that type of algebra used multiple variables. So, a different approach was needed. A different type of mathematics. Boolean Algebra turned out to be the chosen one. Why? Because the variables used in Boolean Algebra were only 2! → true or false. So, it was easy to use binary digits as these variables and use Boolean Algebra to solve the problem in hand. 1 was chosen to hold the 'true' value while 0 held the 'false' value. Remember, the computer still only understands electric voltage. We chose the values to be able to use a method for solving. So now, when we mean true, it means a high voltage for a computer, and when we mean false, it means a low voltage for a computer. Now, let's understand how Boolean Algebra would help us solve problems. 

Boolean Algebra is logic based mathematics devised by George Boole to provide a true/false proof for statements. The solution was based on making logical arguments for a certain expression (which has to be simplified to a final answer) and assigning a true/false variable to each argument based on if it is actually true or false. Finally performing certain operations on arguments (or variables that represent the argument) for the final output. There are three fundamental operations in Boolean Algebra: AND, OR, NOT. Each of these operations requires Boolean inputs (the true/false variables) and give the true/false output based on the rules of operation (similar to how multiplication takes numbers and multiplies them). We choose what operation to be performed (similar to how we choose to add or multiply).

A description based on rules for each operation:

AND: returns a true only and only if both input values are true.

OR: returns a true if at least one input is true.

NOT: takes a single input and returns the opposite as output. 

The circuits for these operations are known as 'Logic gates' and are the fundamental block of computer problem solving and are explained later in the article (memory of a computer is connected to logic gates!). 

Programming Languages - Past and Future: 

In the 40's computers were used primarily to reduce effort in world war and the computers could only perform arithmetic operations and so the machines were designed based on the type of problem to be solved using it. The problem was later fed to the computer using machine code. Machine code is binary code written based on the computer's internal design. Since binary digits (0 and 1) are voltages (low and high), it was easy to control the input using electrical switches. The programs had to be first written in English (the program at this level was called pseudo-code) and then converted to machine code manually.

This conversion was done by hand based on some opcode (operation code) tables. An opcode is a single instruction which the circuit could execute. The opcode tables contained keywords(the instruction) which specified the operation to be performed and the binary translation of these keywords. Early programmers had to specify the memory addresses (like an address A_1 would mean the value stored in that location on the circuit register) of the numbers/values because the computers were incapable of working with variables (modern day programmers could just write A=12 and use A rest of the time without worrying about the actual location of the variable). Opcode commands came to be known as mnemonics. An opcode table should make it easier to understand:

Since this process was tedious, by the late 1950's programmers came up with higher level languages which were more human intelligible. Opcodes were named operands and could be used in statements. So instead of coding out in binary, programmers could give statements like 'ADD LOAD A_16 AND LOAD A_15' (no variables yet so manually instruct the computer to load a value stored in a particular address). However, computers still cannot understand any language but binary. But being the persistent beings humans are, they solved this issue by coding some programs in binary (so that computers can understand it directly). These programs read the text based statements of higher languages and converted them into binary. In a way, these programs 'assembled' higher level code into binary, and so we're known as assemblers. These assemblers enabled the programmer to write more sophisticated code and worry less about computer mechanics and avoid or hide unnecessary details (abstraction of details). 

Since memory addresses still had to be used, updating code became a problem. Adding a little value meant making quite a lot of changes into the actual code and if a value isn't needed you couldn't delete it without making a lot of changes. Considering the still developing circuits, even a little unused value would mean significant power usage by the circuit. Dr. Grace Hopper, an US naval officer who worked upon HARVARD MARK 1 computer during world war 2, wanted to make computers a greater necessity and developed a high level language called A-0. This language used variables and was way advanced than any of the high level languages ever came into existence prior to it. 

So now, programmers could type something like 'A=15; B=23; C=A+B; '. This made it way easier to write more sophisticated codes without worrying about the memory addresses or the circuitry. 

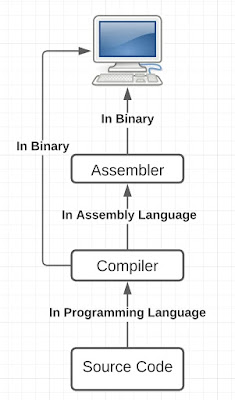
However, assemblers could not 'assemble' it since it used statements which required multiple binary level functions to be used for a single keyword of A-0 language. Assemblers can only convert when a direct conversion of assembly code into binary code is available, both of which mean the same thing and just are written differently. This wasn't the case with A-0 and so a new program named a compiler was made, which could convert the A-0 written code (known as source code) into assembly language which could be converted by an assembler into binary code. Modern day compilers can directly convert the source code in a language to binary code. 

This was so advanced, in fact, that her co-workers were skeptical and  would not use this language believing that computers could only do arithmetic and not actual programs, and so this language died out quickly.

Another genius Alan Backus who worked at IBM (leading computer manufacturing company of that time) developed a new language named Fortran and a compiler for this language. In 1957, this language could be used on IBM computers. This was a major hurdle as no common programming language existed which could be used by everyone on any computer. A committee was made in 1959, to develop a common business oriented programming language and thus COBOL language was born. Because of non uniformity in the architecture of circuitry of different computers, a different compiler was needed but these compilers accepted the same COBOL source code. This opened up opportunities of innovation as computers started to be used for a variety of tasks. This also invoked mass involvement in choosing programming as a career.

As computer hardware advanced, programming languages got better, faster, and easier with time. With ALGOL and BASIC in the 60's, C and SMALLTALK (one thing I'm bad at) in the 70's, C++ and Objective C in the 80's, Python and JAVA in the 90's, it doesn't feel like language design would ever end. So many languages have been developed in the 21st century alone, it feels like the process would only end with us thinking and a code for it being written in the future, making everyone a programmer (what would I do then? Quit my job?) . The CPU circuits still only understand binary and are based on that however. So, never forget what the device you're reading this on is doing for you internally! 

So, to sum up, a flowchart of how a source code in a modern programming language gets converted for machine to understand would look something like this:

Programs, Circuits, and Arithmetic:

Anshuman, I get a little bit now, but how do these programs in the form of binary codes get executed by the computer?! How do computers calculate using electric signals?!! (Remember logic gates?)

Now we come to the most intriguing and clever part of it all. The fundamentals of computer science! Ladies and gentlemen, I present to you …. Logic Gates! 

Logic gates are the induction of Boolean operations in circuitry. These are actual little blocks physically present in your device. Different combinations of logic gates make RAM (temporary computer memory). Let's understand how logic gates (or the operations) actually work. The three main logic gates are AND, OR, NOT named after the operations they perform. Since there are less number of possible output/input cases for the gates and all of the gates take true/false {1/0 in circuit use} as inputs and return true/false outputs {1/0 (high/low voltage) as circuit output}, an output based input table (known as truth table) can be made for these and would look something like this:

(Keep in mind the description of the respective operations)

Truth table for AND gate:

Truth table for OR gate: 

Truth table for NOT gate is pointless since it just reverses the input.

An XOR gate is a gate formed by combination of NOT, OR, AND gates. Truth table for an exculsive OR (XOR) gate is as below.

A NOR gate is a gate formed by combining NOT gate and OR gate. The truth table is as below:

An XNOR gate is another such gate which has a NOT gate with XOR gate and so it produces just the opposite results than XOR. The truth table is below:

Now, imagine we already know of the hardware used to make these gates.(that thing would require a separate article).

These gates when combined in different combinations, produce adder, subtractor circuits, memory circuits, and can perform all sorts of arithmetic. 

Let's take an adder circuit as an example ( the actual circuit diagram would get too complex for the article).

It would take as many inputs as long as they don't exceed 4 binary digits of data. The maximum number which can be represented using 4 bits is 15 in decimal system.

We can make 4-bit adders, 8-bit adders and so on. A 4-bit adder means it can take 4 binary digits as inputs. Similarly an 8-bit adder can take 8 binary digits as inputs. But that does not mean an 8-bit adder is only twice as good than a 4-bit one. An 8 bit adder has 4 more digits t than a 4 bit one and since, in a Base 2 system, each bit holds 2 times the value than the previous bit, the maximum number which can be represented using 8 bits is 255. The conversion process of binary to decimal numbers, hence looks something like this :

So how do modern computers represent millions of digits? They use higher bit and n number of processors.

Simply put, the number of bits typically refers to the length of the character representation that is used to build instructions or data. 4 bits permit 64 distinct characters usage while 8 bits permit 256 characters or instructions usage.

The modern computer circuits are generally 32-bit or 64-bit.

This is all arithmetic though! How do computers execute programs? Say, light up a screen a certain color.

The thing is, circuits already have a pathway for everything. So there is a path to a pixel (the things that show color) on your screen, it just isn't getting electric connection to light up. Whenever we write a program, the computer performs calculations to find that path and finding that path means completing it. Once the path is complete, electric current is sent to it, and voila, it lights up! The process obviously is a lot of more complicated but this is the basic principle behind it.

So finally! What is the circuit made of? What is the physical device that makes these gates possible? What is it that actually stores the data now that we know how to store data? What is that physical thing which does physical work and so requires physical energy? Well, that would be answered in the next part of the "How Computers Work" series.